Available on May 25, 2024 (click here)

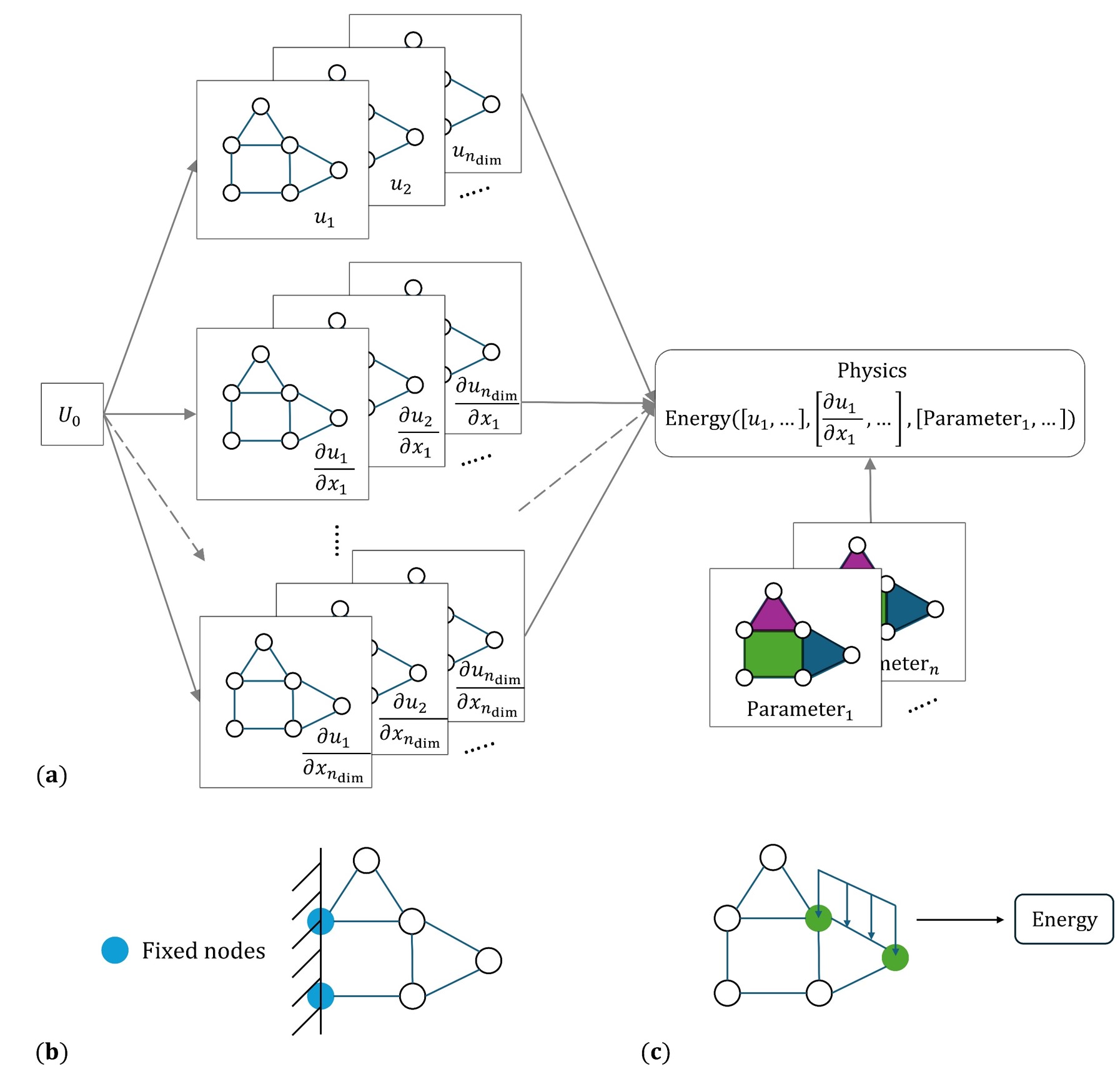
Abstract: Physics-informed neural networks (PINNs) have recently prevailed as a differentiable solver in solid mechanics. However, PINNs have quite limited caliber when dealing with concentration features and discontinuous multi-material heterogeneity, hindering its application as a forward solver for more practical studies. We propose a novel physics-encoded finite element network (PEFEN) that can deal with concentration features and multi-material heterogeneity without special treatments, extra burden, or labeled data. Leveraging the discretized finite element approximation as a differentiable network in the new approach, PEFEN encodes the physics structure of multi-material heterogeneity, functional losses, and boundary conditions. We simulate three typical numerical experiments, and PEFEN is validated with a good performance of handling complex cases where conventional PINNs fail. Moreover, PEFEN entails much fewer iterations (less than one tenth) than some published improved PINNs (namely the mixed form and domain decomposition method), since the proposed PEFEN does not employ extra variables for stresses or special treatments for subdomains. We further examine PEFEN in hyperelastic multi-layer strata with and without a pile, corroborating its ability for more practical applications. It is also discussed that PEFEN may act like domain decomposition in a refined way, and a simple experiment validates that PEFEN can solve the problem with multi-scale frequency. The PEFEN, thus, proves to be a promising method and deserves further development.